Bayes’sche Homöopathie

Wissenschaftlich gesehen kann die Homöopathie als stark datenbasiertes Verfahren betrachtet werden. Zu den meisten Arzneimitteln liegen große Mengen Daten, also Symptome aus Arzneimittelprüfungen sowie aus klinischen Erfahrungen vor.

Wie können diese Daten so aufbereitet und ausgewertet werden, daß sie für die Behandlung bestmöglich genutzt werden können?

Aufgrund der für den Einzelnen unüberschaubaren Menge an Informationen zur den homöopathischen Arzneien gibt es seit den Frühzeiten der Homöopathie Hilfsmittel, den Zugriff auf diese Informationen zu erleichtern und zu strukturieren, in erster Linie in Form von Repertorien. Auch wenn die Entstehungsgeschichte der meisten Repertorien nur bedingt nachvollziehbar ist, so ist doch davon auszugehen, daß ein eher pragmatischer als streng wissenschaftlicher Ansatz gewählt wurde. Allein die Menge der zu verarbeitenden Informationen lässt es extrem unwahrscheinlich erscheinen, daß eine erschöpfende Auswertung auf diesem Wege stattgefunden hat. Zudem erscheint es ohne die Anwendung statistischer Verfahren nahezu aussichtslos, einen objektiven Blick auf diese Datenmengen zu bekommen. Es ist also davon auszugehen, daß die bisherigen Repertorien mit nicht unerheblichen Mängeln behaftet sind.

Das Bayes’sche Theorem hat sich in den letzten 40 Jahren in verschiedensten Wissenschaftsbereichen sehr erfolgreich etabliert. Es handelt sich hierbei um ein statistisches Verfahren, welches den Prozess des menschlichen Lernens aus Erfahrung mathematisch nachvollziehbar und operationalisierbar macht. Diese Übereinstimmung geht soweit, daß einige Neurowissenschaftler vom Bayesianischen Gehirn sprechen. In der menschlichen Wahrnehmung und Erfahrung werden Zusammenhänge – oft (vermeintlich) kausal – in der Regel durch zeitliche und räumliche Nähe hergestellt. Erfährt ein Mensch z.B. wiederholt einen brennenden Schmerz kurz nach der Berührung einer bestimmten Pflanze (Brennessel), so wird er diese Pflanze als Ursache seiner Empfindung ansehen. Je häufiger er diese Erfahrung macht, um höher wird er die Wahrscheinlichkeit (englisch likelihood) einschätzen, daß die Pflanze das Brennen verursacht – ganz ohne Kenntnisse von den chemischen Inhaltsstoffen der Pflanze, dem Aufbau von Hautrezeptoren und dem Mechanismus der Reizung. Macht dieser Mensch im weiteren Verlauf seinen Lebens dann die Erfahrungen, daß es auch Pflanzen mit gezackten Blättern gibt, die nicht brennen (die Taubnessel), so wird dies seine angenommene Wahrscheinlichkeit wieder reduzieren – bis er lernt, die beiden Pflanzen anhand der weißen Blüten zu unterscheiden, und sich die angenommenen Wahrscheinlichkeiten ausdifferenzieren.

Auch in der medizinischen Diagnostik finden diese mentalen Prozesse unentwegt statt. Kommt eine Patientin mit einem akuten Abdomen in die Notaufnahme, so wird das gemessene Fieber eine Reihe von Diagnosen wahrscheinlich machen, ebenso die Leukozytose – eher unspezifische Faktoren, die eine gewisse Grund- oder a priori-Wahrscheinlichkeit für mehrere Diagnosen abschätzen. Ergibt sich in der klinischen Untersuchung ein kontralateraler Loslassschmerz, so steigt die Wahrscheinlichkeit für eine akute Appendizitis sprunghaft an – der Loslassschmerz hat eine sehr hohe likelihood für diese spezielle Erkrankung. Diese inneren Wahrscheinlichkeitsberechnungen resultieren dabei aus der Erfahrung des Behandlers, aber mindestens genau stark aus dem Wissen, das Generationen von Ärztinnen und Ärzten in der klinischen Arbeit und in geplanten Studien gewonnen haben.

Es wird also deutlich, daß sich die Prozesse des Lernens aus Erfahrung unterstützen – und auch korrigieren – lassen, indem die Erfahrungen Anderer hinzugezogen und ausgewertet werden. Genau dies leistet das Bayes’sche Theorem. Im Kern ist es eine Formel, mit der sich für zwei Phänomene die Wahrscheinlichkeit berechnet lässt, daß diese in einem kausalen Zusammenhang stehen. In der Regel handelt es sich hierbei um die Frage der diagnostischen Wahrscheinlichkeit: wir kennen das Symptom (z.B. den Loslassschmerz) und wollen wissen, wie hoch die Wahrscheinlichkeit ist, daß dieses durch eine bestimmte Diagnose bzw. Krankheit (z.B. Appendizitis) verursacht wird.

Auf die Homöopathie angewandt: der Patient hat ein Symptom, und wir wollen für eine Reihe von Arzneien (die eine gewisse a priori-Wahrscheinlichkeit für eine erfolgreiche Behandlung aufweisen) wissen, wie hoch für dieses Symptom die Wahrscheinlichkeit ist, daß die jeweilige Arznei hilfreich sein wird.

Aufgrund der umfangreichen Daten, die aus den Arzneiprüfungen vorliegen, können wir mit der Bayes-Formel den Symptom-Arznei-Zusammenhang quantifizieren, ausgedrückt in Form der Likelihood Ratio. Die Likelihood Ratio, kurz LR, kann auf der Grundlage der Materia medica für jeden Symptom-Arznei-Zusammenhang berechnet werden und ist ein Ausdruck dafür, wie spezifisch ein Symptom für eine bestimmte Arznei ist.

Allerdings ist es dafür wichtig, die gesamte Materia medica auszuwerten. Während bei der Erstellung der bisherigen Repertorien die absolute Zählweise von Symptomen dominierte, ist das Prinzip der Likelihood Ratio ein relatives: Die Häufigkeit eines Symptoms eines Arzneimittels wird immer ins Verhältnis gesetzt – zur Häufigkeit dieses Symptoms überhaupt (also in der gesamten Materia medica) sowie zur Gesamtzahl der Symptome dieses Arzneimittels.

Als vereinfachte Formel ausgedrückt:

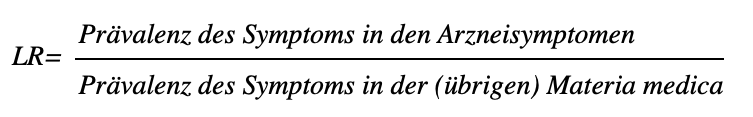
Daraus folgt auch, daß für einen Arznei-Symptom-Zusammenhang nur dann eine hohe LR errechnet werden kann, wenn dieses Symptom in der Gesamt-Materia medica nicht besonders häufig auftritt. Damit bildet das Bayes’sche Theorem eine Kernthese der Homöopathie quantitativ ab: Symptome sind für Arzneiwahl relevant, wenn sie sonderlich, ungewöhnlich sind (§ 153 Organon). Symptome sind ungewöhnlich, wenn sie selten sind. Seltene Symptome haben eine hohe LR.

Die Analyse der Materia medica mit dem Bayes’schen Ansatz ermöglicht ein Repertorium, welches einerseits ein vollständiges Bild des bisherigen Arzneiwissens bietet, und andererseits die charakteristischen Arzneien für jede Rubrik herausarbeitet.

Phenomena, das Repertorium der Phänomene, basiert auf diesem Ansatz. Es ist in der homöopathischen Praxissoftware Analogon verfügbar.


Literatur

Schäferkordt R. Repertorium der Phänomene: Neukonzeption eines vollständig in der Materia medica referenzierten Repertoriums mit phänomenbasierter Struktur und Bayes-Gradierung. AHZ 2021; 226: 16–23

Schäferkordt R. Klinische Verifikation der Materia medica unter Anwendung des Bayes’schen Theorems. AHZ 2014; 259: 24–28

Rutten L, Stolper CF, Lugten RFG. Repertory and likelihood ratio: Time for structural changes. Homeopathy 2004; 93: 120–124

Spies M. Unsicheres Wissen. Wahrscheinlichkeit, Fuzzy-Logik, neuronale Netze und menschliches Denken. Spektrum Akademischer Verlag 1993